Fouriers Theorem and Frequency Domain

Joseph Fourier was an 18th-century French mathematician who was working in writing mathematical equations for a heat field when he formulated a theorem that made it possible to understand the application of frequency analysis to the area of vibration - vibration analysis.

Without getting into the formula etc, we will take some things as mathematical truth and accept them as a fact.

Simply stated - the Fourier theorem provides the mathematical truth that all periodic waveforms can be expressed as the sum of several sine waves. Each of these sine waves has a different frequency and magnitude.

Synthesis is the process when we add several sine waves to make a specific waveform conversely when we break down any waveform into several sine waves, the process is called analysis. An everyday example to illustrate analysis is your radio. The antenna will catch all stations but the tuner by tuning to one specific frequency allows only one station to play at a time.

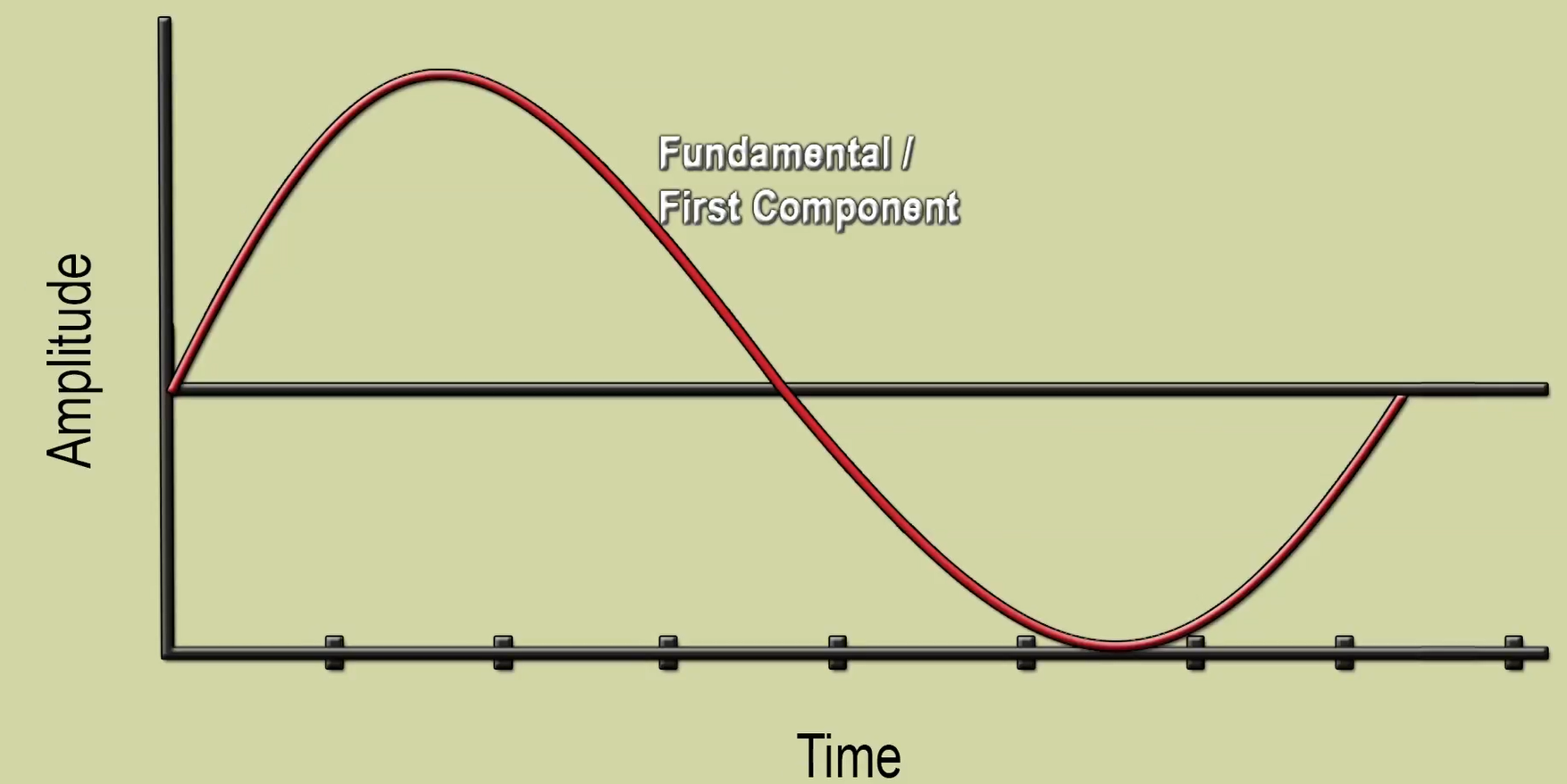
Let's look at a sine wave - this is a pure tone - single frequency and single magnitude signal. We call this the first component.

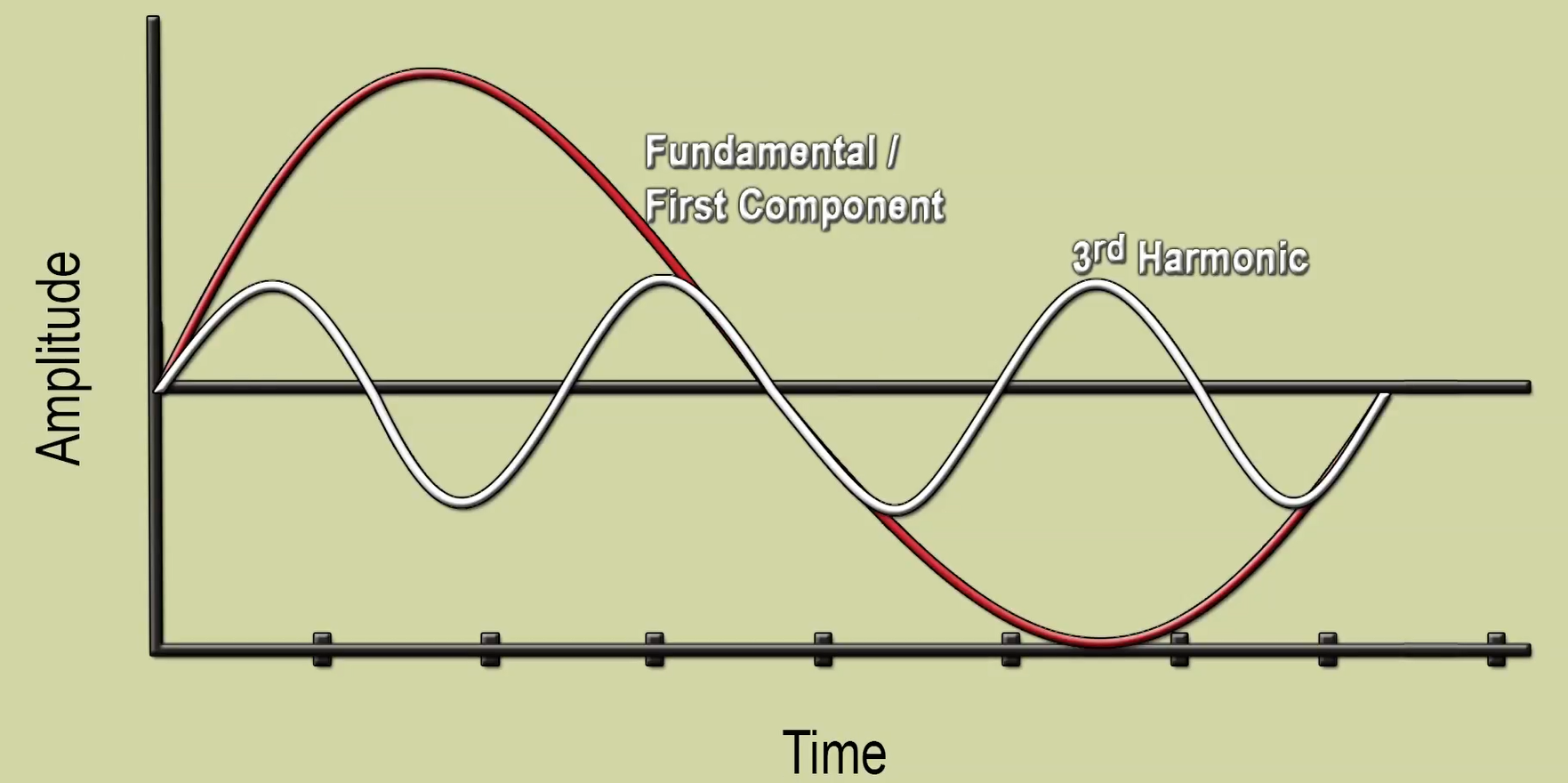
let's look at its third harmonic which means another sine wave having three times the frequency of the first wave with one-third magnitude and add these two waves together


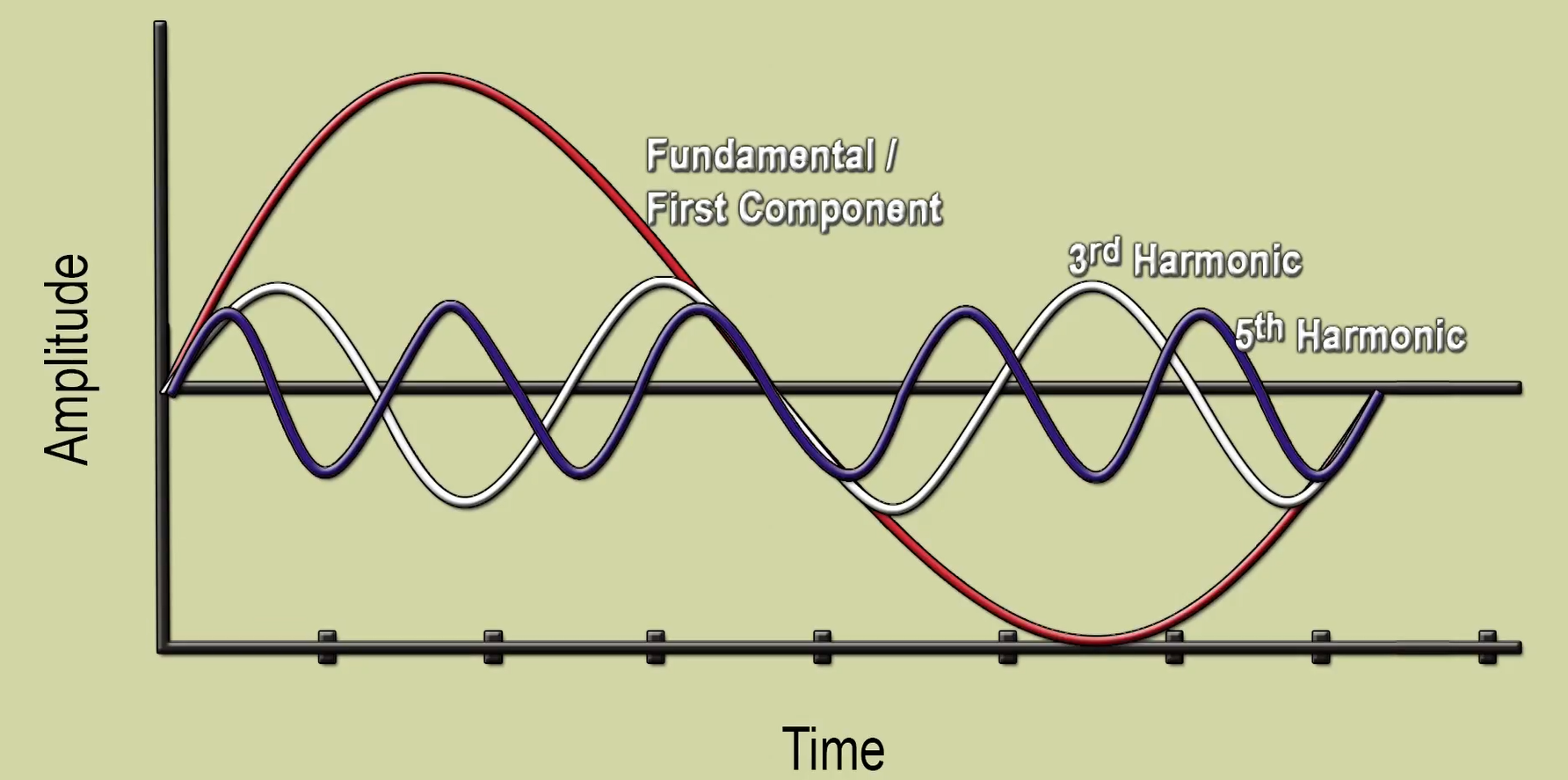
Let’s now take another sine wave with five times the frequency and one-fifth magnitude and add this also.


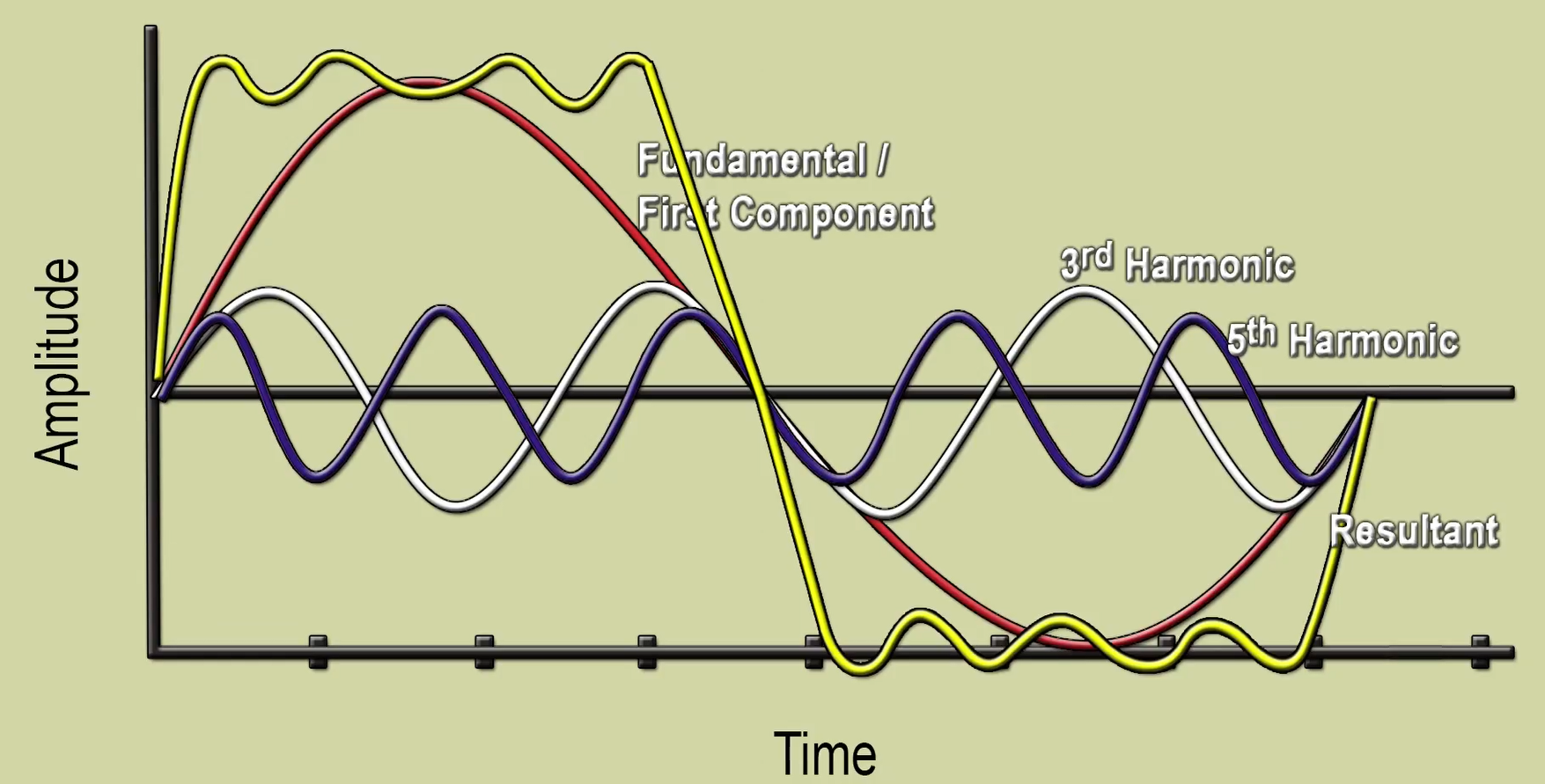
We notice that as we add these waves together, we get almost a square wave.

If we generalize this principle - any wave can be expressed as a sum of several sine waves of different frequencies and amplitudes. Conversely, any wave can be broken down into a series of sine waves.

Once we have all the different frequency components of a vibration signal, we can plot a curve between amplitude and frequency. We would have then gone into what is called the frequency domain which is also referred to as the frequency spectrum.

In a frequency spectrum, we see the presence of several signals of different frequencies as peaks. The position of the peak along the x-axis is the frequency and its height is the magnitude.

Remember that the frequency of the cause in forced vibration is always the same as the frequency of the effect of the vibration. Therefore, if you find the dominance of a certain frequency in the frequency spectrum of a machine we can and then look for the cause which would logically have the same frequency. In this process, we require very powerful analytical tools to diagnose the causes of vibration in a machine.

Baseline Technologies was established in 1990, and offers Portable Instruments for measurement of Sound and Vibration, including analysis, monitoring, field-balancing, and custom measurement solutions in the above areas.

Vibration measurement, Condition Monitoring based on frequency- analysis, and In- position dynamic balancing of rotors: these are the three most commonly faced applications of vibration in machinery.

BASELINE VIBRATION ANALYSER cum DYNAMIC BALANCER 6050 offers solutions to all these three applications in a single, portable, rechargeable battery-operated unit that fits into a briefcase.
Learn More: https://www.baselinetechno.com/